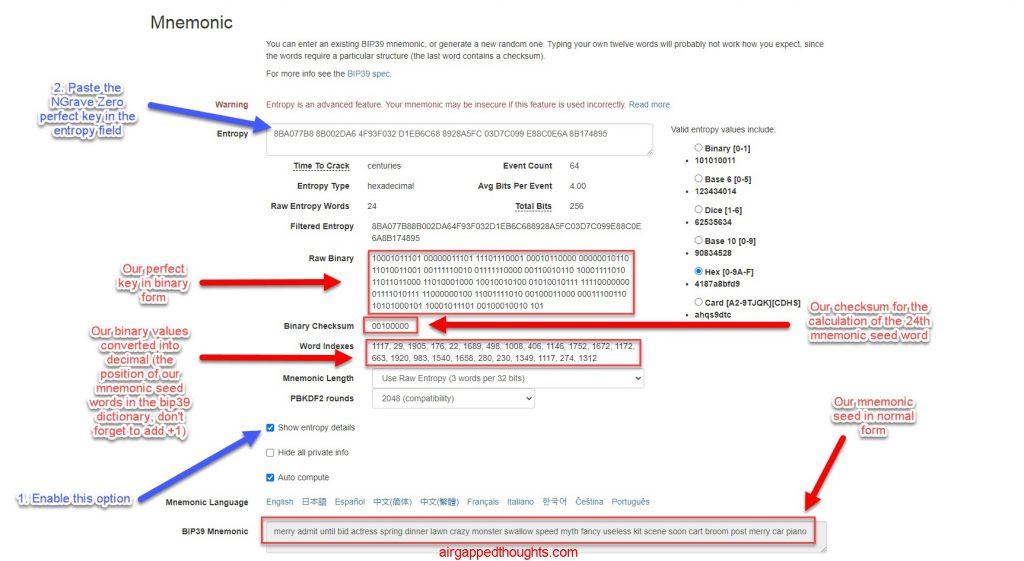
NGrave Zero is using a different approach to generate mnemonic seeds using the hexadecimal system (all numbers (0-9) and A-F letters), although normal seeds are also supported. It’s not hard to figure out the whole process as long as you know how normal mnemonic seeds are generated (there’s a detailed article about mnemonic seeds here, i wont put the same amount of detail in this article). In this article we are going to generate a perfect key and see the whole process step by step. Generated seed is for testing purposes only and shouldn’t be used by you or you’ll probably end up losing your funds. Online tools should only be used for testing purposes and not with your actual seed.
GENERATING THE NGRAVE KEY
Let’s go and generate a random seed.
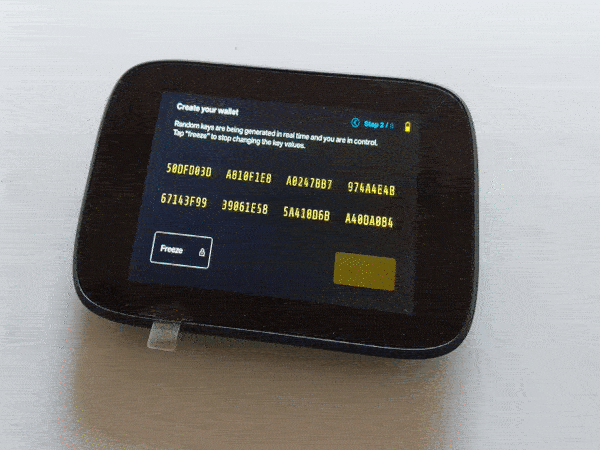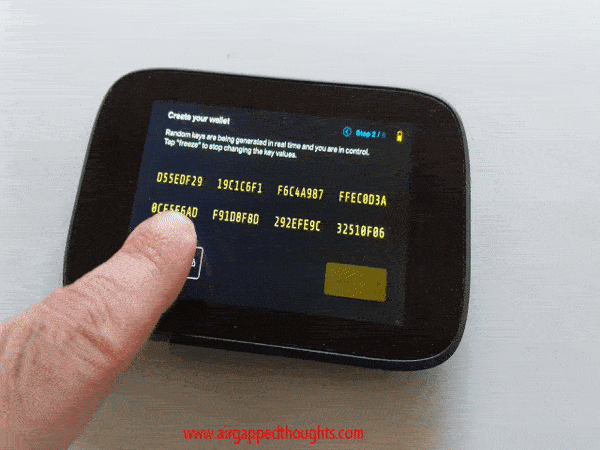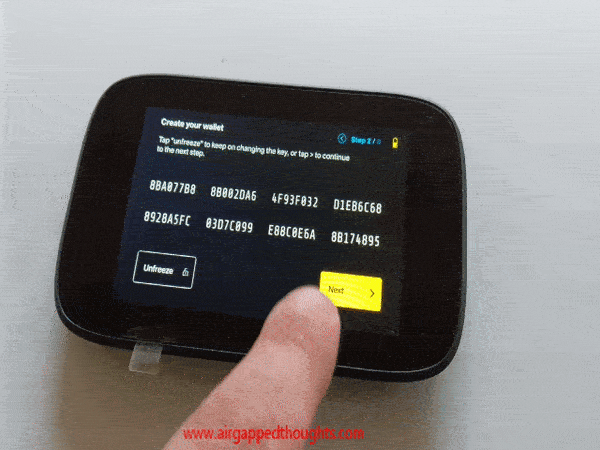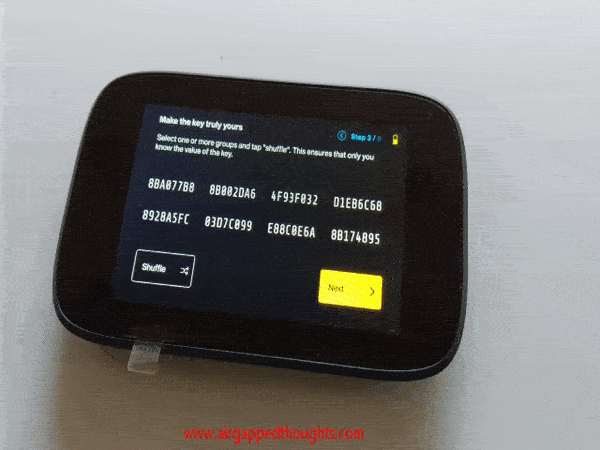
8BA077B8 8B002DA6 4F93F032 D1EB6C68 8928A5FC 03D7C099 E88C0E6A 8B174895
- Mnemonic seeds have a fixed number of bits. NGrave Zero is using 24 word mnemonic seeds, these are generated using 264 bits of information (264 0 and 1) of which the 256 are randomly generated, and the rest 8 are calculated based on the other 256.
- Each mnemonic seed word is 11 bit long, covering all possible 0 and 1 combinations from 00000000000 (first mnemonic seed word from bip39 dictionary) up to 11111111111 (last mnemonic seed word from bip39 dictionary).
- NGrave perfect key is using the hexadecimal system. In hexadecimal system, each digit represents 4 bits of information. NGrave perfect key is 64 digits long (8 parts of 8 digits each) which equals to 64 digits. Multiply 64 with 4 bits of info each and we have 256 bits. This is an indication that the perfect key doesnt contain the checksum / 24th word (cause 24 words are 11 x 24 = 264 bit long), it only contains the random words part. The checksum is calculated in the background and is not a part of our Graphene backup (it can be calculated manually by you, and if you want to import your perfect key to NGrave, it will also calculate the rest 8 bits so don’t worry about that. You can also view the normal mnemonic seed via the Settings of the device)
So, our generated perfect key is:
8BA077B8 8B002DA6 4F93F032 D1EB6C68 8928A5FC 03D7C099 E88C0E6A 8B174895
Let’s remove all the spaces between each part.
8BA077B88B002DA64F93F032D1EB6C688928A5FC03D7C099E88C0E6A8B174895
Now we’re going to use a hexadecimal to binary calculator to turn our perfect key into 0s and 1s. For the purpose of this article you can use this online tool. The conversion will give us the number:
1000101110100000011101111011100010001011000000000010110110100110010011111001001111110000001100101101000111101011011011000110100010001001001010001010010111111100000000111101011111000000100110011110100010001100000011100110101010001011000101110100100010010101
Let’s split it into parts of 11 bit each since every mnemonic seed word is 11 bit long.
10001011101 00000011101 11101110001 00010110000 00000010110 11010011001 00111110010 01111110000 00110010110 10001111010 11011011000 11010001000 10010010100 01010010111 11110000000 01111010111 11000000100 11001111010 00100011000 00011100110 10101000101 10001011101 00100010010 101
We’re now having 23 parts of 11 bit each, and a 24th part with just 3 bit. Which equals to 23 mnemonic seed words and we need to calculate the last 8 bit ourselves for the 24th word which will play the role of the checksum. These steps were necessary to understand the process, we will actually take a step backwards and use the hex format of our seed (the perfect key) to calculate our checksum. So take the perfect key and use this online tool to hash it using sha256. To do so, paste it into the Binary Hash field, press the Hash button, scroll down and grab the SHA-256 result. For our perfect key, the result is:
20b29741245bdfff4808b6513ddc3c7e8dcf7c24a528df8670d1dad0c8be5a5a
Notice the first two digits of our result, this is our mnemonic seed checksum, we will use it to calculate the 24th word. So take these first 2 bytes and turn them into binary using this online tool. The result will be 00100000
Now take these 8 bits and stick them next to the last 3 bits of our mnemonic seed:
10001011101 00000011101 11101110001 00010110000 00000010110 11010011001 00111110010 01111110000 00110010110 10001111010 11011011000 11010001000 10010010100 01010010111 11110000000 01111010111 11000000100 11001111010 00100011000 00011100110 10101000101 10001011101 00100010010 10100100000
This is our 24 words mnemonic seed. Turn each one of these parts into decimal using this online tool, and add 1 in the result.
10001011101 = 1117 + 1 = 1118
00000011101 = 29 + 1 = 30
11101110001 = 1905 + 1 = 1906
00010110000 = 176 + 1 + 177
00000010110 = 22 + 1 = 23
11010011001 = 1689 + 1 = 1690
00111110010 = 498 + 1 = 499
01111110000 = 1008 + 1 = 1009
00110010110 = 406 + 1 = 407
10001111010 = 1146 + 1 = 1147
11011011000 = 1752 + 1 = 1753
11010001000 = 1672 + 1 = 1673
10010010100 = 1172 + 1 = 1173
01010010111 = 663 + 1 = 664
11110000000 = 1920 + 1 = 1921
01111010111 = 983 + 1 = 984
11000000100 = 1540 + 1 = 1541
11001111010 = 1658 + 1 = 1659
00100011000 = 280 + 1 = 281
00011100110 = 230 + 1 = 231
10101000101 = 1349 + 1 = 1350
10001011101 = 1117 + 1 = 1118
00100010010 = 274 + 1 = 275
10100100000 = 1312 + 1 = 1313
Finally, go to the bip39 dictionary, and find the corresponding numbers.
1118 = merry
30 = admit
1906 = until
177 = bid
23 = actress
1690 = spring
499 = dinner
1009 = lawn
407 = crazy
1147 = monster
1753 = swallow
1673 = speed
1173 = myth
664 = fancy
1921 = useless
984 = kit
1541 = scene
1659 = soon
281 = cart
231 = broom
1350 = post
1118 = merry
275 = car
1313 = piano
This is our mnemonic seed in its normal form. Don’t forget that if you go to the Settings of the Zero, you can see the normal form too and not just the hexadecimal format. You can also use the Iancoleman BIP39 Mnemonic Code Converter to calculate it (here or here for the offline version). Just enable the “Show entropy details”option to make the “Entropy” field appear and paste the NGrave Zero perfect key in it to automatically have everything calculated for you.
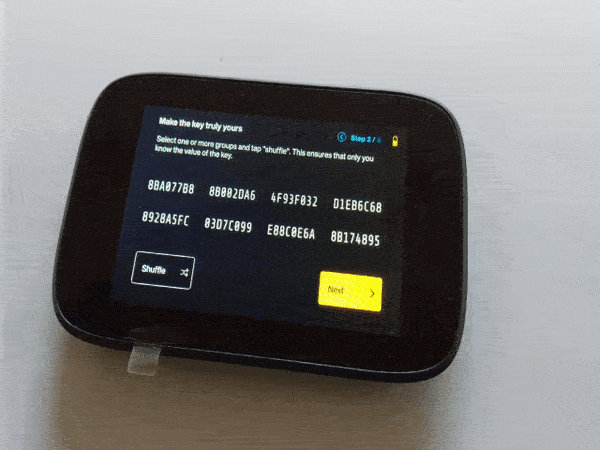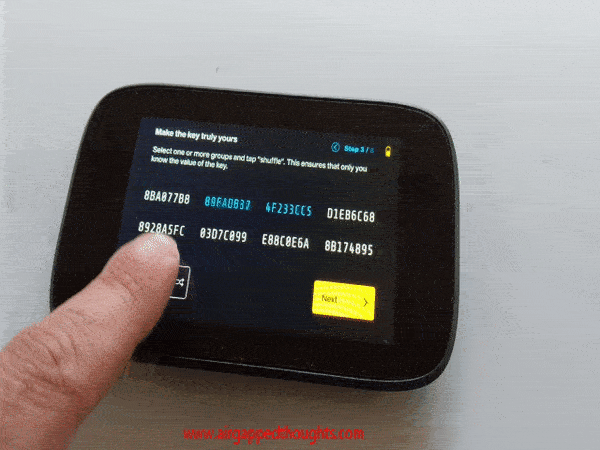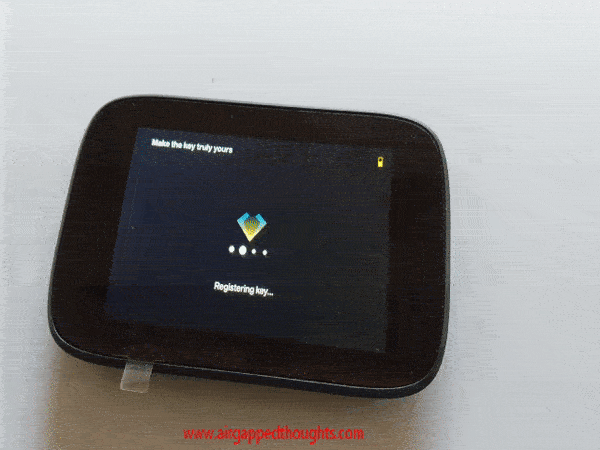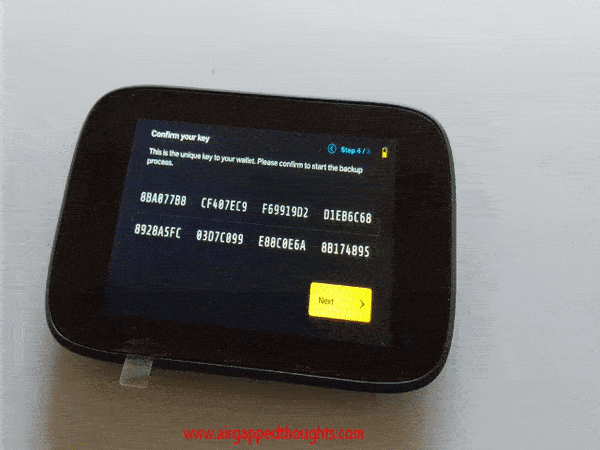
NGrave will also let you shuffle the perfect key values which will change the result of our mnemonic seed. Let’s see an example with the above perfect key.
SHUFFLING THE NGRAVE KEY
Our original perfect key was:
8BA077B8 8B002DA6 4F93F032 D1EB6C68 8928A5FC 03D7C099 E88C0E6A 8B174895
Now let’s take the 2nd and 3rd part and shuffle them a few times.
8BA077B8 CF407EC9 F6991902 D1EB6C68 8928A5FC 03D7C099 E88C0E6A 8B174895
Shuffled parts turned into CF407EC9 F6991902. What shuffle actually does though the name is a bit misleading is to generate new 0s and 1s. It doesn’t shuffle our generated words, it creates new ones. Makes sense because each one of the 8 hexadecimal parts that we can shuffle is 32 bits which means that they have info for more than 2 words but less than 3 (remember that each word is 11 bits) which means that info for some of these words is getting split between two sequential parts and so they cannot get shuffled without getting a very different result. Depending on the number of shuffled parts, the generated seed will have little to no relation to the original, but the checksum (the last word) will almost always be different cause SHA-256 value will be different.
Now let’s go and play with our shuffled hexadecimal seed:
8BA077B8 CF407EC9 F69919D2 D1EB6C68 8928A5FC 03D7C099 E88C0E6A 8B174895
Remove spaces, and get the sha256 value for our checksum with this tool.
8BA077B8CF407EC9F69919D2D1EB6C688928A5FC03D7C099E88C0E6A8B174895
SHA-256 value of above hexadecimal seed is:
925e669a19289090437a2233a8e2d958fae2c3ba9cb783518fb32eff198ce3b0
Turn the first two bytes into decimal with this tool:
92 turns into 10010010, that’s our checksum.
Let’s turn the shuffled seed into binary with this tool, and add above checksum in the end.
100010111010000001110111101110001100111101000000011111101100100111110110100110010001100111010010110100011110101101101100011010001000100100101000101001011111110000000011110101111100000010011001111010001000110000001110011010101000101100010111010010001001010110010010
Split it into parts of 11 bit each.
10001011101 00000011101 11101110001 10011110100 00000111111 01100100111 11011010011 00100011001 11010010110 10001111010 11011011000 11010001000 10010010100 01010010111 11110000000 01111010111 11000000100 11001111010 00100011000 00011100110 10101000101 10001011101 00100010010 10110010010
Turn each part into decimal with this tool, and add 1
10001011101 = 1117 + 1 = 1118
00000011101 = 29 + 1 = 30
11101110001 = 1905 + 1 = 1906
10011110100 = 1268 + 1 = 1269
00000111111 = 63 + 1 = 64
01100100111 = 807 + 1 = 808
11011010011 = 1747 + 1 = 1748
00100011001 = 281 + 1 = 282
11010010110 = 1686 + 1 = 1687
10001111010 = 1146 + 1 = 1147
11011011000 = 1752 + 1 = 1753
11010001000 = 1672 + 1 = 1673
10010010100 = 1172 + 1 = 1173
01010010111 = 663 + 1 = 664
11110000000 = 1920 + 1 = 1921
01111010111 = 983 + 1 = 984
11000000100 = 1540 + 1 = 1541
11001111010 = 1658 + 1 = 1659
00100011000 = 280 + 1 = 281
00011100110 = 230 + 1 = 231
10101000101 = 1349 + 1 = 1350
10001011101 = 1117 + 1 = 1118
00100010010 = 274 + 1 = 275
10110010010 = 1426 + 1 = 1427
Finally, let’s turn these numbers into words using the bip39 dictionary.
1118 = merry
30 = admit
1906 = until
1269 = ozone
64 = among
808 = gossip
1748 = surprise
282 = case
1687 = spot
1147 = monster
1753= swallow
1673 = speed
1173 = myth
664 = fancy
1921 = useless
984 = kit
1541 = scene
1659 = soon
281 = cart
231 = broom
1350 = post
1118 = merry
275 = car
1427 = rather
This is our ‘shuffled’ mnemonic seed. You can also verify it through the Settings of NGrave Zero (Display secret key / Mnemonic wallet).


Notice that by shuffling 2nd and 3rd part of the perfect key, 6 words got affected in the final result (words 4 – 9) and all the others stayed the same as in the non shuffled mnemonic seed (except for the checksum / last word of course). 3rd word could have been affected too but in this example it did not. Let’s see why:
32 BITS VS 11 BITS
As i said, each one of the 8 parts that can be shuffled represent 32 bits of information and each mnemonic seed word has 11 bits of information. When we shuffled the 2nd and 3rd part, we’ve interacted with all bits from 33rd – 96th. Let’s take the original seed in its binary form and visualize the 2nd and 3rd parts of the NGrave Zero perfect key, before the shuffling (the orange digits represent the second perfect key part (bits 33 – 64) and the blue digits represend the 3rd perfect key part (bits 65 – 96):
10001011101 00000011101 11101110001 00010110000 00000010110 11010011001 00111110010 01111110000 00110010110 10001111010 11011011000 11010001000 10010010100 01010010111 11110000000 01111010111 11000000100 11001111010 00100011000 00011100110 10101000101 10001011101 00100010010 10100100000
Notice that we are interacting with every bit of the 4th, 5th, 6th, 7th and 8th word (which means that they’ll definitely gonna change) but not all bits from words 3 and 9. And although we are interacting with most bits of the 9th word, we are only interacting with just 1 bit of the 3rd word (the 33rd bit of the mnemonic seed). If that shuffle turned that bit into 0, then the 3rd word would have been different since it would go from 11101110001 to 11101110000 (which equals to 1904 + 1 = 1905 = “unlock” word instead of “until”). But shuffling just 1 bit from a word means just a 50% of a chance to change since we only have 2 results for every bit, either 0 or 1. For the 9th word, although we didn’t shuffle all of its bits, 8 out of 11 are good enough to provide 28 = 256 different combinations or 1/256 probability to get the same 9th word.
Notice how the last bit of the 3rd word (the green digit) stayed the same before and after the shuffle.
ORIGINAL SEED
10001011101 00000011101 11101110001 00010110000 00000010110 11010011001 00111110010 01111110000 00110010110 10001111010 11011011000 11010001000 10010010100 01010010111 11110000000 01111010111 11000000100 11001111010 00100011000 00011100110 10101000101 10001011101 00100010010 10100100000
SHUFFLED SEED
10001011101 00000011101 11101110001 10011110100 00000111111 01100100111 11011010011 00100011001 11010010110 10001111010 11011011000 11010001000 10010010100 01010010111 11110000000 01111010111 11000000100 11001111010 00100011000 00011100110 10101000101 10001011101 00100010010 10110010010
IS THIS KEY REALLY PERFECT?
As you’ve seen, there’s nothing too magical in the whole process. Perfect keys are a way to mix binary values while adding support for a cryptographic backup solution (the Graphene). Even without the Graphene, it’s a bit safer to have these lying around (don’t do that) instead of having notes with readable mnemonic seed words. On the other hand, it’s easier to make a mistake when copying these values in a paper so you have to be double careful and double check your backup. Even without the graphene backup, i’d still go with these till we get another way of interacting with values (like the dice roll feature) but backing up hex values could be a bit too much for some.
No matter what, have fun playing with these values and don’t forget to experiment in the crypto world before adopting something new for serious usage.


