I’ve already posted an article on how to create a mnemonic seed manually. Now we are going to learn to create our own bitcoin keys. You’d probably thought that the creation of a mnemonic seed which gives countless keys would be harder than the creation of a single key but unfortunately you’d be wrong. Manually creating a bitcoin key is much harder because you’ll have to go through more advanced cryptographic functions but hopefully we have some awesome tools to help us through this lengthy process.
Lets do this.
TOOLS WE ARE GOING TO NEED DO NOT USE ONLINE PAGES FOR ANYTHING ELSE THAN TESTING. WHENEVER I RECOMMEND AN ONLINE PAGE IS FOR YOUR CONVENIENCE WHILE PLAYING WITH THE KEYS ON THIS PAGE OR WHENEVER YOU WANNA EXPERIMENT WITH DUMMY KEYS
Hexprobe Multibyte Calculator (for hashing operations and conversions between hexadecimal and other formats)
Secp256k1 Calculator (requires Java) (for elliptic curve calculations, required for calculating our public key)
BITCOIN PRIVATE KEY CREATION
Creating a bitcoin private key is actually very ease since all we have to do is to create a random value. Our value can be anything between 0x1 and 0xFFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFE BAAE DCE6 AF48 A03B BFD2 5E8C D036 4140 which transforms as 1.1578e77 or (take a deep breathe) 115.792.089.237.316.195.423.570.985.008.687.907.852.837.564.279.074.904.382.605.163.141.518.161.494.336.
We do not need a binary number like in the mnemonic seed process, we can take as an entropy whatever we want and we will hash it through the SHA-256 function. As an entropy we could use random words, random keystrokes, or even gibberish. Of course none of that is recommended, for this example i will just type some randomly 1 and 0 but the recommended way is to use a password generator which has the ability to create entropy from user interaction (like Keepass):
0100101000101010101010010010101010101010010010110100101010110101010101100010100010110101010101011010101101010101101010000010100111010101101010101010101101100101011010101010010110101010101010101010101101010100100110101010101010101100110101010101000001111111111110000000100101000101111101010101010101101010101010101010101011010101010001011010101001010101
Remember that you can literally get a private key from anything, just type something long enough. Now we are going to hash it through SHA-256. The result for the above binary value is:
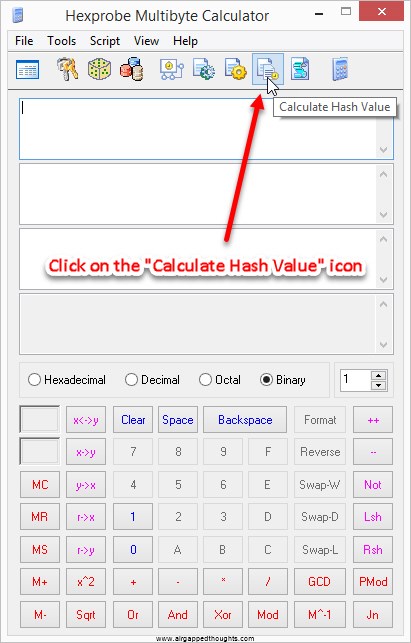
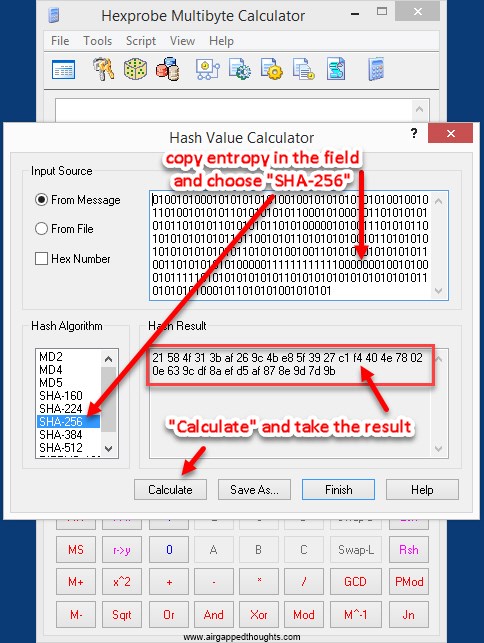
21584f313baf269c4be85f3927c1f4404e78020e639cdf8aefd5af878e9d7d9b
You can also use this online tool (do not use online tools for anything else than testing) and type your entropy inside the “String hash” field and press the “Hash” button. Go to the bottom of the page and take the “SHA-256” value.
No matter what we used as an entropy, sha-256 will always give us a 32 bytes hexadecimal value which is exactly what we want. This is our private key but it’s not in its final form. First we have to make sure that our key is inside the allowed limits so we just convert the above hex value to decimal and compare it with the number 115.792.089.237.316.195.423.570.985.008.687.907.852.837.564.279.074.904.382.605.163.141.518.161.494.336.
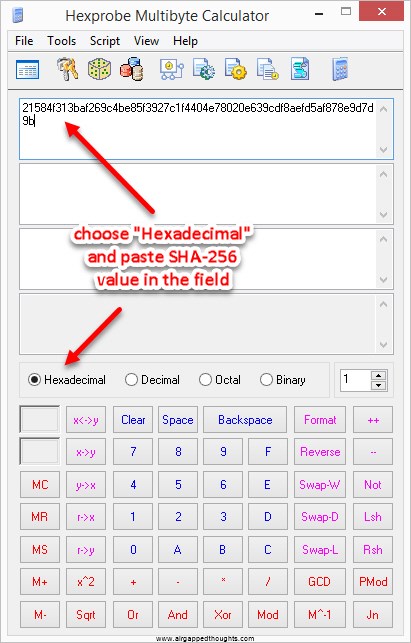
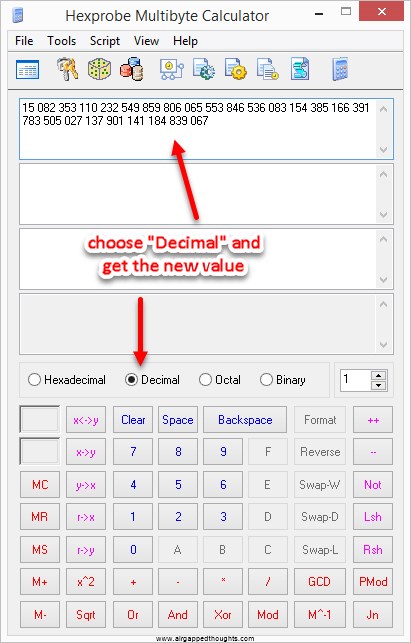
Our decimal value is:
15.082.353.110.232.549.859.806.065.553.846.536.083.154.385.166.391.783.505.027.137.901.141.184.839.067
You can also use this online tool for the conversion from Hexadecimal to Decimal
Its obvious that our value is much shorter so we don’t even have to make a compare and we can move on. If our number was bigger from the limit, we would have to make a new entropy. The probability of getting a bigger number is close to zero but we always have to check.
Now that our private key is valid, we need to convert it to a bitcoin frienly format. We use a prefix in front of the private key depending on the format we want to get, for an uncompressed bitcoin addresses we use the prefix 80. So our private key now becomes:
8021584f313baf269c4be85f3927c1f4404e78020e639cdf8aefd5af878e9d7d9b
We now need a checksum. To get it, we will double SHA-256 the above value and take the first 8 bits from the result. If you want an online tool you can use this one again but now you will have to use the “Binary hash” field.
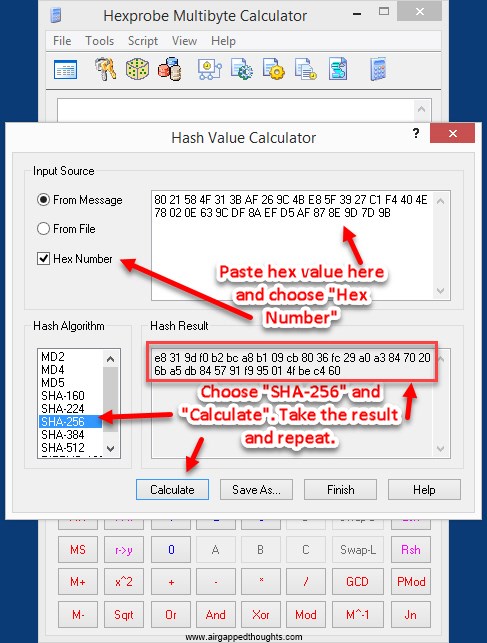
1st SHA-256 value is e8319df0b2bca8b109cb8036fc29a0a38470206ba5db845791f995014fbec460 we hash this value and the next result is:
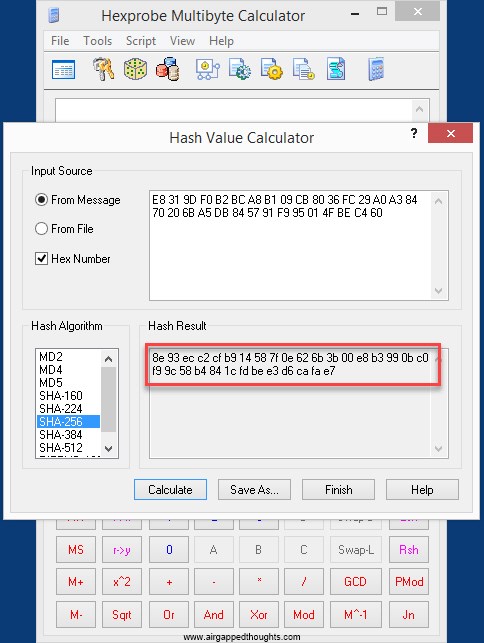
8e93ecc2cfb914587f0e626b3b00e8b3990bc0f99c58b4841cfdbee3d6cafae7
We take the first 8 bits from the second value and add it to the end of our private key (the one with the 80 prefix) so now we should have:
8021584f313baf269c4be85f3927c1f4404e78020e639cdf8aefd5af878e9d7d9b8e93ecc2
There’s only one conversion left to get the valid form of our private key, a Base58 conversion.
You can use this online tool. Just don’t forget to change the “Treat Input As” to HEX.
(unfortunately i could’t find an offline gui tool for this, if i find one i will update the article, remember not to use online tools for keys that you are actually going to use)
The result is our private key!
5J4yLJsvGHmsk2KP5mqnYN97FUGDxkC8AP8SCABLVCwc2Gh4av5
If we want to get a compressed private key (starts with K or L) we need to double SHA-256 the same hex value as before with the addition of 01 in the end:
8021584f313baf269c4be85f3927c1f4404e78020e639cdf8aefd5af878e9d7d9b01
which would give us a totally different result / checksum:
1966dface4ab83290c35df87f4f7f45a593e38ac392ef714db8d37078b19e400
We add the checksum to the end of our hex value:
8021584f313baf269c4be85f3927c1f4404e78020e639cdf8aefd5af878e9d7d9b011966dfac
Which in base58 is going to give us the private key:
KxLXeDuk6V34xtp8U4vL1SJnasLCD3e6cQfpCFWd1Vi1aLM2wt6u
Most crypto private keys are generated as simple as that, we just have to know the prefix that we will have to use to end up with a valid result and use some other encryption than SHA-256.
BITCOIN PUBLIC KEY CREATION
You’re probably familiar with the fact that you can go from a private key to a public key but not the other way around. The reason why that happens is because bitcoin and most cryptocurrencies are making use of the elliptic curve cryptography and most specifically the elliptic curve that is defined by Secp256k1 format.
Elliptic curves satisfy the equation y^2=x^3+ax+b and for secp256k1 we have a=0, b=7 and also a base point (G) with which we just multiply our private key and end up with our public key. Let’s see a very basic example of how multiplications in the elliptic curve happen:
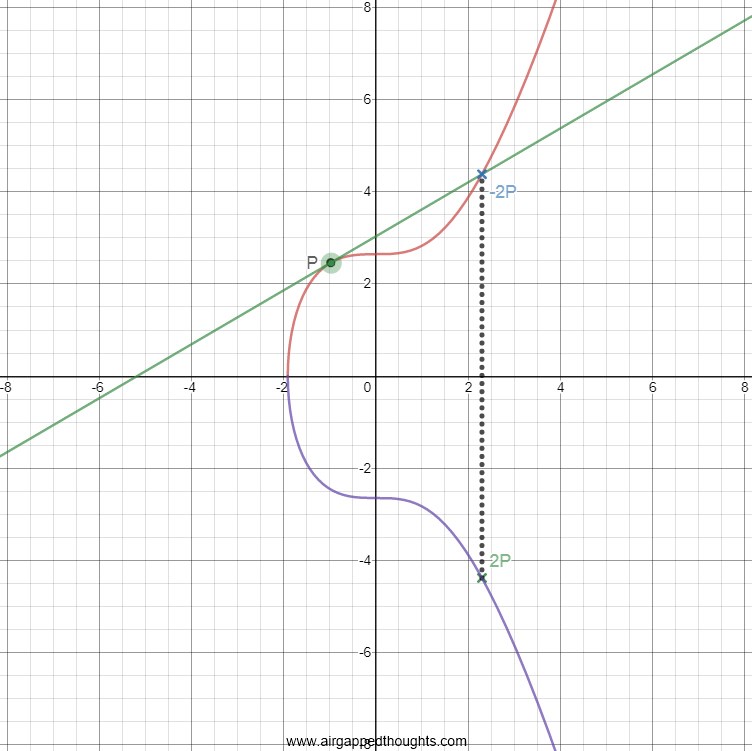
In the above picture we are doing a simple P*P multiplication. To do this, we draw a tangent line through P point and we extend it till it touches our curve (the –2P point in the picture). When it touches it, we reflect that point through the x-axis and the final point is the one we are looking for (2P). That wasn’t so bad so let’s do an example with 2 multiplications (P*P*P or 2P*P).
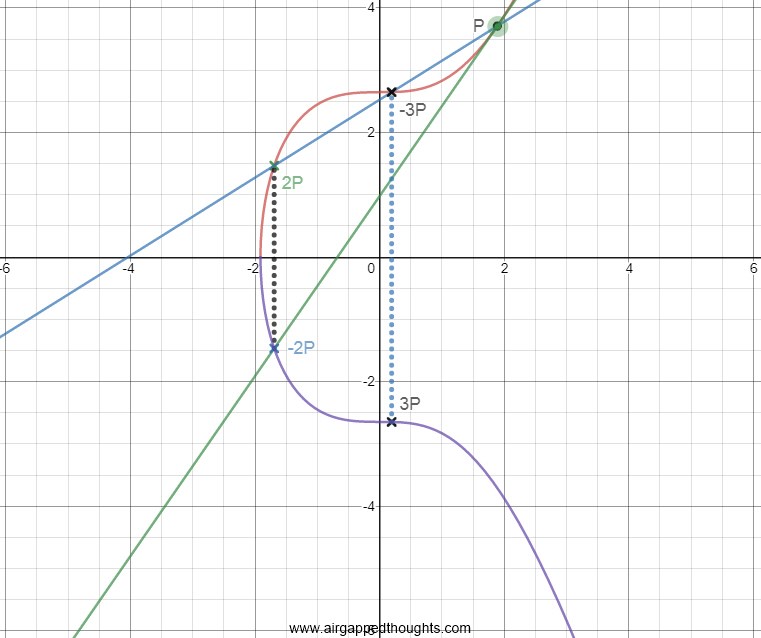
For the first multiplication we do the same thing, a tangent line that starts from the first point till it touches our curve, and mirror that point through the x-axis to get the 2P point. Then we are doing a P*2P multiplication. We draw a tangent line from P through the 2P point, and the point that we touch in between is our -3P point. We reflect through x-axis and we got our 3P point.
It’s already a bit of a mess so multiplying our private key with the base point can only get worse. When we finally get to the final point (which will be our public key), there is no way to compute how we got there, the answer to that is our private key. (Don’t forget that our public key is the secp256k1 base point (G)*Private Key)
This of course is a very simplified explanation. Also when i said in the beginning of this article that we have to make sure that our private key wont be larger than a specific value, it’s because elliptic curves have this limitation and you wont be able to compute a public key for a larger private key.
Let’s move on and calculate the public key for our private key. Our private key was:
21584f313baf269c4be85f3927c1f4404e78020e639cdf8aefd5af878e9d7d9b
We will use the Secp256k1 Calculator (don’t forget to install Java)
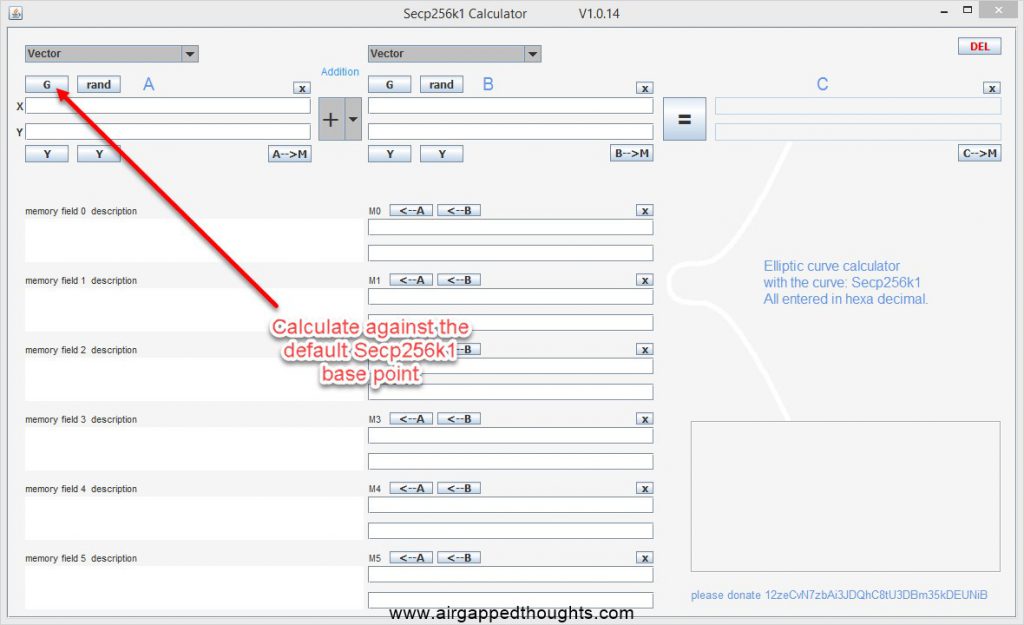
In the first screen, you will have to use the default x,y coordinates for the base point in which our private key will get multiplied. Just press the ‘G’ button to have the values auto filled.
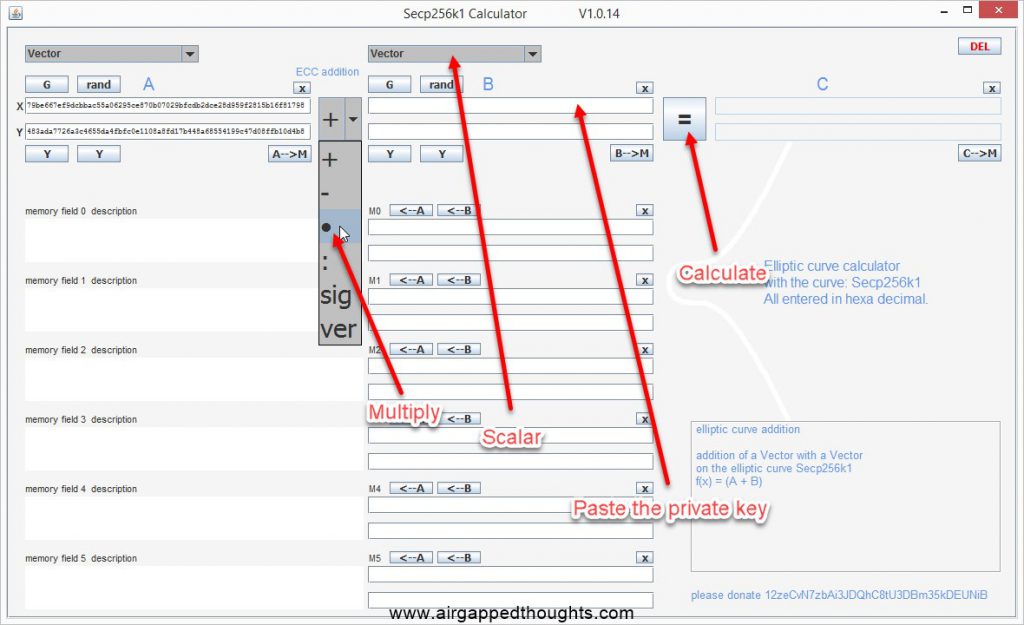
Change the above parameters. From addition to multiplication, from vector to scalar, paste the private key inside the scalar field (you will only have one field after choosing scalar), and finally, press the calculate button.
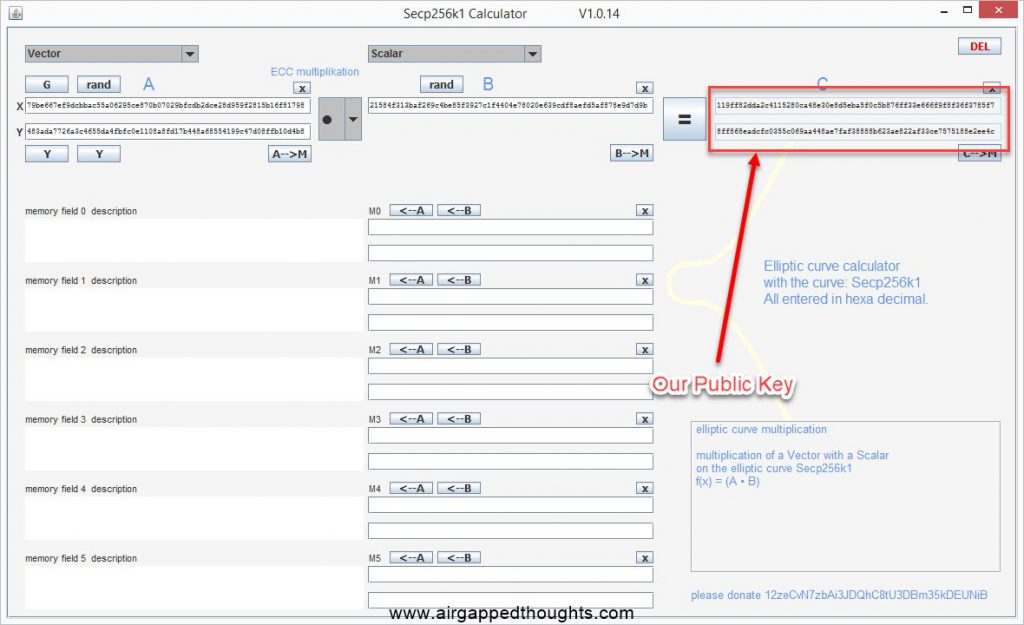
These two values are our public key. That’s because a public key is actually the x and y coordinates on the elliptic curve.
Our x value is: 119ff82dda2c4115280ca48e30e8d5eba5f0c5b876ff33e666f9f8f36f3785f7
Our y value is: 8ff868eadcfc0355c069aa448ae7faf38888b623ae822af33ce7575188e2ee4c
Both of these values together are our public key:
119ff82dda2c4115280ca48e30e8d5eba5f0c5b876ff33e666f9f8f36f3785f78ff868eadcfc0355c069aa448ae7faf38888b623ae822af33ce7575188e2ee4c
This is an uncompressed public key. When we use an uncompressed public key, we put the prefix 04 in front of it:
04119ff82dda2c4115280ca48e30e8d5eba5f0c5b876ff33e666f9f8f36f3785f78ff868eadcfc0355c069aa448ae7faf38888b623ae822af33ce7575188e2ee4c
==========================================================
We can also create a compressed public key by completely removing the y value since its easily calculated from the x value. If the y value is an odd number, we just write the x value with the 02 prefix in front, otherwise we put a 03 prefix, for example:
02119ff82dda2c4115280ca48e30e8d5eba5f0c5b876ff33e666f9f8f36f3785f7 or 03119ff82dda2c4115280ca48e30e8d5eba5f0c5b876ff33e666f9f8f36f3785f7
==========================================================
Back to our uncompressed key. We have to turn it into a public address before we can use it. To do that, we first SHA-256 our key.
04119ff82dda2c4115280ca48e30e8d5eba5f0c5b876ff33e666f9f8f36f3785f78ff868eadcfc0355c069aa448ae7faf38888b623ae822af33ce7575188e2ee4c and it will turn into:
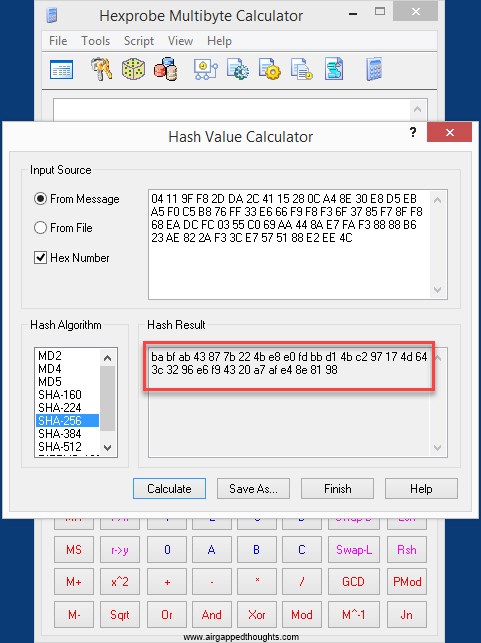
babfab43877b224be8e0fdbbd14bc297174d643c3296e6f94320a7afe48e8198
Now we have to hash the new value through RIPEMD-160, the result is:
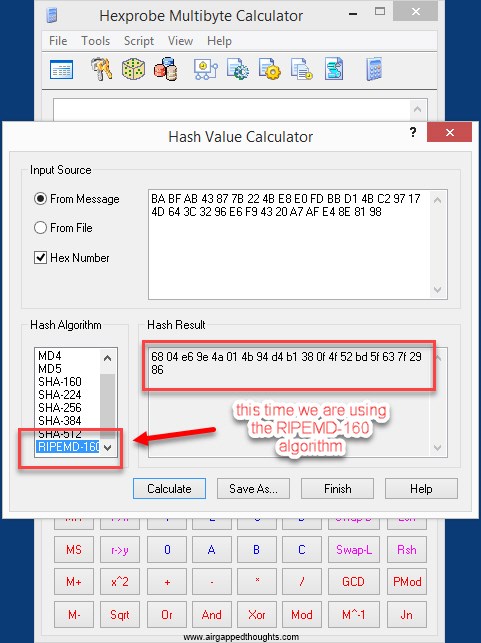
6804e69e4a014b94d4b1380f4f52bd5f637f2986
Add 00 in front of it
006804e69e4a014b94d4b1380f4f52bd5f637f2986
Now we need a checksum and so we double SHA-256 the above value and get the first 4 bytes from the result:
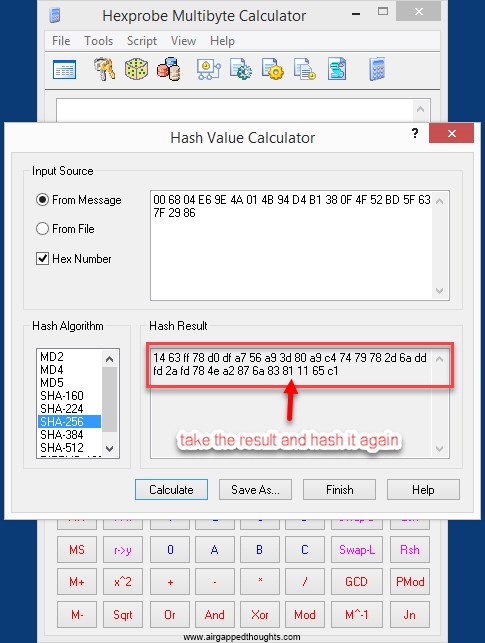
1463ff78d0dfa756a93d80a9c47479782d6addfd2afd784ea2876a83811165c1
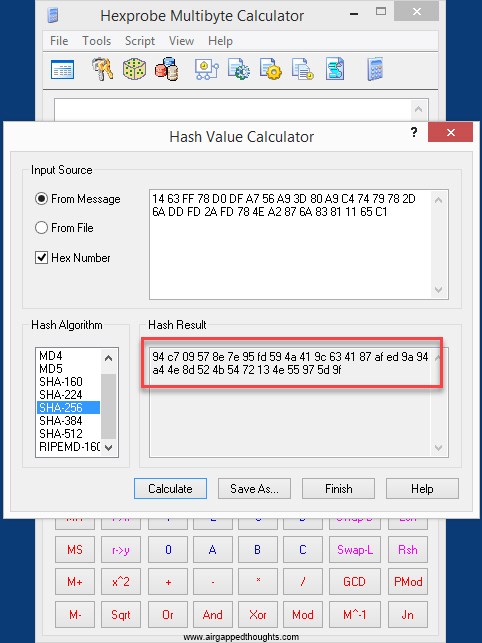
94c709578e7e95fd594a419c634187afed9a94a44e8d524b5472134e55975d9f
We take the checksum and paste it at the end of our public key:
006804e69e4a014b94d4b1380f4f52bd5f637f298694c70957
And we can finally convert it to Base58 and get our Public Address:
1AV19U7xcE1hr2vPuGKP1wX6BfH4HuFSf8
Of course you don’t have to do a private key to public address conversion by yourself. If you import your private key to a wallet it will immediately calculate the public address for you and if you don’t want to use your private key to a wallet, you can use tools to calculate it like the bitaddress.org website, there’s an option at the top “Wallet “Address” to test your dummy private keys but you can also download the offline version of the website at the bottom of the page (direct link here).
Also keep in mind that many people generate entropy using simple words. If you create entropy using words like “Bitcoin” or “Satoshi Nakamoto”, you will get bitcoin private keys that have been used. Don’t do it!
Have fun!


